长沙培训Day1
昨天晚上做了一个奇怪的梦,梦见今天考试怒得5分稳稳垫底。然后考试一开始看到第一题有20个测试点,当时就吓尿了。
第一题:
给出一个无限大的矩阵,每个格子的值c如下给出:
I、1 (x==0||y==0)
II、c[x-1][y]+c[x][y-1] (else)
求从[0][0]到[n][m]的一条路径,使得这条路径上的点权和最小,输出点权和mod 10^9+7
(m,n<=10^12,m*n<=10^14,时限1s)
-------------------------------------------------------------------------------------------------------------
第二题:
给定一个非负整数序列{a},初始长度为N。
有M个操作,有以下两种操作类型:
1、A x:添加操作,表示在序列末尾添加一个数x,序列的长度N+1。
2、Q l r x:询问操作,你需要找到一个位置p,满足l<=p<=r,使得:
a[p] xor a[p+1] xor ... xor a[N] xor x 最大,输出最大是多少。(m,n<=300000,时限2s)
----------------------------------------------------------------------------------------------------------------------------
第三题:
一家公司需要雇佣一些工人来进行生产。
在他们手里有N个可以雇佣的工人资料,这些工人有些曾经合作过,他们
在一起工作能够使公司利润更大,而有些工人素未谋面,不能给公司带来什么额
外的收益。我们用P(i,j)来衡量i 工人和j 工人一起雇佣能给公司带来的收益,P
越大公司收益越高。
当然,公司雇佣工人需要支付薪金;然而,在这里公司需要支付的薪金并不
与雇佣的人数成正比,而是满足:C=K*(200-K)。其中C表示需要支付的薪金,
K表示雇佣的人数。
现在,为了让公司能够有最多的获利,需要最大化G=S/C,其中S表示雇佣
的工人两两P(i,j)之和,C表示公司需要支付的薪金。
(n<=50,时限1s)
-------------------------------------------------------------------------------------------------------------
第二第三题交的都是朴素。第一题想+写了两个小时,用到乘法逆元,加了很多惨无人道的优化之后ac时间排到第一。好高兴。
然后总分就rank9了- -
-------------------------------------------------------------------------------------------------------------
官方题解:
一、
观察原图,将x+y值相同的点(x,y)归为一层,将层按x+y值从小到大看,会发现其实整个图是杨辉三角的一部分。
容易看出,每层权值最小的点或都在最左侧或都在最右侧。由于N,M互换并不影响答案,所以假如每层权值最小的点都在最右侧,则交换N,M,保证每层权值最小的点都在最左侧。
从本质上说,就是该图的最短路是确定的,都是沿着矩形外围一圈走,且一开始先走矩形长的一边。(下述C均为组合数)
保证N<=M,那么答案可以直接算出,也就是M+C[M][0]+C[M+1][1]+…+C[M+N][N]。
C[M][0]=1;
C[M+1][1]=(M+1)/1;
C[M+2][2]=(M+1)*(M+2)/(1*2)=C[M+1][1]*((M+2)/2);
C[M+3][3]=C[M+2][2]*((M+3)/3);
…
C[M+N][N]=C[M+N-1][N-1]*((M+N)/N)。
由于模的数是一个素数,所以除以数a直接转化成乘数a的逆元。接着直接递推即可。
【注:这里的算法不是最优的。容易知道sigma(C(i,a),i=[1,b])=C(b,a+1)。那么效率顿时就提高了很多。】
==============================================================
二、
可以用线段树套字母树做到O(Nlog^2N),下面讲O(NlogN)的做法。
首先对原序列求前缀异或和,记为S[i]。则对于询问l,r,x,则是在S[l-1]..S[r-1]这些数中找到一个数,和X异或的结果最大。
要使异或结果最大,可以从高位到低位看X的二进制位,如果该位为1,则我们需要找这些数中是否存在该位为0的。
假如我们将S[l-1]..S[r-1]这些数按照二进制从高到低的顺序看做字符串,并做出这些字符串对应的字母树,那么我们可以在O(log)时间内解决问题。
问题在于如何快速查找S[l-1]..S[r-1]形成的字母树的信息,并且支持在序列末尾添加的操作。
由于我们在字母树查询的只是“该结点是否存在至少一个在[l-1,r-1]范围的数”,而[l-1,r-1]的个数是满足区间减法的。也就是说,如果我们知道[0..r-1]以及[0..l-2]在该节点的个数,那么我们可以通过区间减法得到[l-1,r-1]的信息。
即我们需要对每个位置X,维护[0,X]的字母树,而注意到[0,X]到[0,X+1],在字母树上只添加了一个字符串,修改的结点个数不会超过O(log);而我们利用函数式编程的思想,每次修改并不在原结点修改,而是新建一个修改过的结点。这样我们可以保留这个字母树的历史版本,可以在O(NlogN)的时间内解决这道题。
时间复杂度:O(NlogN)。空间复杂度:O(NlogN)。
【注:第一次见到用trie来做数字统计类题目的。函数式的思想很棒。此题有人朴素得了50分。膜拜常数帝。】
=============================================================
三、
题目需要使得 sigma(P)/(K*(200-K)) 最大。
首先,我们可以二分答案X,那么我们需要判断的是,是否存在点集,使得sigma(P)/(K*(200-K)) > X。
我们对式子做以下变形:
我自然的想到将边权重新赋值为P(i,j)+2*X,将点权赋值为-199X,那么问题转换成在新图上选出一个点集,使得导出子图的点权与边权的和最大。
解决的方法之一是将其转换成最大权闭合子图的模型:
我们构造一个新图以转换模型,原图中的一个点u对应新图中的一个点u,点权不变;对于原图中的边e(u,v),对应新图中点e,点权为原图的边权,并且新图中e点向u点和v点连接有向边,表示若选择e,则u和v也一定被选。
然后我们在求出新图的最大权闭合子图就可以判断是否能够满足sigma(P)/(K*(200-K)) > X这个式子了。
【注:这题的01分数规划模型很明显,但是可惜考场上没有成功转化为最小割。毕竟题目做得太少。这题有人贪心AC,有人写了个随机模拟爬山法也AC了。当时考场上怎么没想到随机呢- -】
-------------------------------------------------------------------------------------------------------------
食堂的菜逐渐变得不那么辣。挺好吃的。这里的人说话口音好重。
-------------------------------------------------------------------------------------------------------------
听说总分前20会有T恤。希望能有。期待明天的考试。
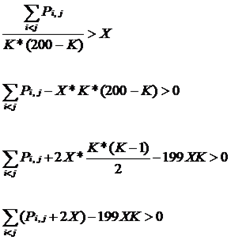
 评论 (0)
评论 (0)