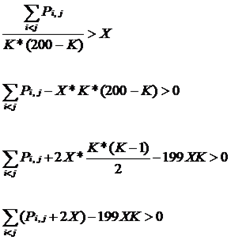#include <jystream>

以奇怪的姿势到了NOI

六道题目一道提交答案剩下四道签到题一道码农题

提答只搞到了26分

签到题被卡了一道常数

码农题在dp的时候设的初始值太小了挂成30分

然后就以奇怪的姿势滚粗了

SAD

给定字符串，判断L是否为其循环节：L-前缀与L-后缀比较即可

如果需要枚举某个数的因数使得该因数满足某一条件，而且该条件如果a不满足那么任意d|a均不满足

可以一个个质因数分解过来搞

问题：给定数列A[]，若干询问，每次给定X，求有多少A[i]&X=X

值域与n同阶

暴力枚举子集要O(3^(logn))

可以这么搞

	for(i=0;i<20;++i)
	for(j=0;j<=N;++j)
	if(j&(1<<i))b[j-(1<<i)]+=b[j];

复杂度靠谱

每次询问O(1)

背代码如下

XOR:+,-

AND:+, 

OR: ,+

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int a[100001],ta[100001];
int b[100001],tb[100001];
int c[100001],tc[100001];
int pusu[100001];
void fwt(int x[],int l,int r)
{
	if(l+1==r)return;
	int mid=(l+r)>>1;
	fwt(x,l,mid);
	fwt(x,mid,r);
	for(int i=l;i<mid;i++)
		x[i]+=x[i-l+mid];
}
void rfwt(int x[],int l,int r)
{
	if(l+1==r)return;
	int mid=(l+r)>>1;
	for(int i=l;i<mid;i++)
		x[i]-=x[i-l+mid];
	rfwt(x,l,mid);
	rfwt(x,mid,r);
}

需要注意：1、区间左开右闭 2、原地执行算法

用这种写法上FFT好像挺科学的。。

http://cdqz.openjudge.cn/2015/1050/

考虑一个数组A[1..n],求:sigma(i,j=1..n:gcd(A[i],A[j]))=sigma(i,j=1..n:sigma(d|A[i]&&d|A[j]:μ(d)))=sigma(d=1..n:μ(d)*cnt[d]*cnt[d])，其中cnt[i]表示A[]数组中i的倍数的数的个数

考虑莫队算法

问题变成加/减一个数，同时维护答案

考虑到这里的d只能是新加进的数A[t]的因子，再配合cnt和预处理的μ数组可以搞

10000以内的数最多只有64个因子，所以是O(64msqrt(n))的效率

别人的题解：http://www.cnblogs.com/oldmanren/p/3661936.html

看不太懂，不知道是不是这意思

有这个方法的话就可以搞一些莫名其妙让人第一眼摸不着头脑的区间询问题了

最近做了SCOI2014GDOI2014

觉得智商还是有问题

看到一种牛逼的决策单调优化

def work(L, R, dl, dr) :
    m = (L + R) / 2
    for i = dl to dr :
        update g[m] using i
    if L == R : return 
    let dm be the optimal decision of m
    work(L, m - 1, dl, dm)
    work(m + 1, R, dm, dr)

定义x的半必经点为某个x在DFS树上的祖先y，且保证在y---x路径上删除除端点外的任意一点后仍然存在路径从y到x，令semi(x)为所有y中dfn最小的

考虑半必经点定理：

对于一点y，x∈pre(y)：

①dfn[x]<dfn[y]，x即为y在DFS树上的祖先，根据定义：if(dfn[x]<dfn[semi[y]])semi[y]=x;

②dfn[x]>dfn[y]，x不为y的祖先，此时对于任意x的祖先z，满足dfn[z]>dfn[y]：if(dfn[semi[z]]<dfn[semi[y]])semi[y]=semi[z]

这里有几个地方需要解释一下

一、为什么要dfn[z]>dfn[y]：考虑u=lca(x,y)，x所属的是一个较晚被dfs到的子树，如果某个z是x的祖先，且dfn[z]<dfn[y]，那么此时z必为y在DFS树上的祖先，那么直接将z删去便可使semi(z)无法到达y，与定义不符

二、这样子获得的semi[y]一定为y的祖先么：x所属的子树较晚被dfs到，故获得的semi必为y的祖先

必经点定理相当直观，不叙述

这玩意就算考也不会太难吧。。。

whoknows

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
#define NN 100001
#define MM 1000000
struct chain
{
	int ver[NN],next[MM<<1],to[MM<<1],tot;bool f[MM<<1];
	void addedge(int from,int t,bool v)
	{next[++tot]=ver[from];to[tot]=t;f[tot]=v;ver[from]=tot;}
}G,dom;
int dfn[NN],clk,idom[NN],semi[NN],fa[NN],id[NN];
struct Ufs
{
	int p[NN],best[NN];
	int getf(int x)
	{
		if(x==p[x])return x;
		int t=getf(p[x]);
		if(dfn[semi[best[x]]]>dfn[semi[best[p[x]]]])best[x]=best[p[x]];
		p[x]=t;
		return p[x];
	}
	int getbest(int x)
	{getf(x);return best[x];}
}ufs;
int n,m;
void dfs(int o)
{
	dfn[o]=++clk;id[clk]=o;
	for(int i=G.ver[o];i;i=G.next[i])
		if(!dfn[G.to[i]]&&G.f[i])
		{fa[G.to[i]]=o;dfs(G.to[i]);}
}
bool flag[NN];
void read(int& a)
{
	static char t;
	t=getchar();a=0;
	while(t<'0'||t>'9'){t=getchar();}
	while(t>='0'&&t<='9')
	{a=a*10+(t-'0');t=getchar();}
}
int main()
{
//	scanf("%d%d",&n,&m);
	read(n);read(m);
	for(int i=1;i<=m;i++)
	{
		int a,b;//scanf("%d%d",&a,&b);
		read(a);read(b);
		G.addedge(a,b,1);
		G.addedge(b,a,0);
	}
	dfs(1);
	for(int i=1;i<=n;i++)ufs.p[i]=i,ufs.best[i]=i,semi[i]=i;
	for(int i=n;i>1;i--)
	{
		int tmp=2100000000;
		for(int t=G.ver[id[i]];t;t=G.next[t])
		{
			if(G.f[t])continue;
			if(dfn[semi[ufs.getbest(G.to[t])]]<tmp)
			{
				tmp=dfn[semi[ufs.getbest(G.to[t])]];
			}
		}
		semi[id[i]]=id[tmp];
		dom.addedge(semi[id[i]],id[i],1);
		for(int t=dom.ver[fa[id[i]]];t;t=dom.next[t])
		{
			if(dfn[semi[ufs.getbest(dom.to[t])]]<dfn[fa[id[i]]])
				idom[dom.to[t]]=ufs.getbest(dom.to[t]);
			else idom[dom.to[t]]=semi[dom.to[t]];
		}
		dom.ver[fa[id[i]]]=0;
		ufs.p[id[i]]=fa[id[i]];
	}
	semi[1]=1;idom[1]=0;
	for(int i=2;i<=n;i++)
		if(idom[id[i]]!=semi[id[i]])
			idom[id[i]]=idom[idom[id[i]]];
	int ans=0;
	for(int i=2;i<=n;i++)
		if(!flag[idom[i]]){++ans;flag[idom[i]]=true;}
	
	printf("%d\n",ans);
	for(int i=1;i<=n;i++)
		if(flag[i])
		{
			ans--;
			if(ans==0)printf("%d\n",i);
			else printf("%d ",i);
		}
}

马上就要day2了

好快啊

http://vfleaking.blog.163.com/blog/static/17480763420123301447215/

感觉起来好像非二维情况根本没法推广的样子？

在分治的时候经常要还原并查集

用这个方法

struct UFS
{
	int fa[NN];
	int a[MM*10],b[MM*10],cnt;
	void save(int x)
	{++cnt;a[cnt]=fa[x];b[cnt]=x;}
	int getf(int x)
	{
		if(fa[x]==x)return x;
		int i=x,j;
		while(fa[x]!=x)x=fa[x];
		while(fa[i]!=i)
		{
			j=fa[i];
			save(i);
			fa[i]=x;
			i=j;
		}
		return x;
	}
	void merge(int a,int b)
	{
		int pa=getf(a),pb=getf(b);
		if(pa==pb)return;
		save(pa);p[pa]=pb;
	}
	void recover()
	{
		while(cnt)
		{
			p[b[cnt]]=a[cnt];
			cnt--;
		}
	}
}ufs;

http://www.tsinsen.com/ViewGProblem.page?gpid=A1342

http://www.tsinsen.com/ViewGProblem.page?gpid=A1313

构造某种可以二分的C

#include <cstdio>
#include <cstdlib>
#include <cmath>
const double pi=acos(-1);
struct complex
{
	double real,imag;
	complex(double a=0,double b=0){real=a;imag=b;}
};
complex operator + (const complex& t1,const complex& t2)
{return complex(t1.real+t2.real,t1.imag+t2.imag);}
complex operator - (const complex& t1,const complex& t2)
{return complex(t1.real-t2.real,t1.imag-t2.imag);}
complex operator * (const complex& t1,const complex& t2)
{return complex(t1.real*t2.real-t1.imag*t2.imag,t1.real*t2.imag+t1.imag*t2.real);}
inline int reverse(int v,int n)
{
	int ans=0;
	for(int i=0;i<n;i++)
		ans+=(1<<i)*(v>>(n-i-1)&1);
	return ans;
}
void fft(complex target[],const complex from[],int n,int rev)
{
	int len=1<<n;
	for(int i=0;i<len;i++)target[i]=from[reverse(i,n)];
	for(int i=1;i<=n;i++)
	{
		int d=1<<i;
		complex wn=complex(cos(2*pi/d*rev),sin(2*pi/d*rev));
		for(int j=0;j<len;j+=d)
		{
			complex w=complex(1,0);
			for(int k=j;k<j+d/2;k++)
			{
				complex t=target[k],p=target[k+d/2]*w;
				target[k]=t+p;target[k+d/2]=t-p;
				w=w*wn;
			}
		}
	}
	if(rev==-1)
		for(int i=0;i<len;i++)
			target[i].real/=len;
}

FFT有各种神奇的用法

还可以分块呢呢呢呢呢呢呢呢呢呢

orz卢教

http://discuss.codechef.com/questions/39948/gerald07-editorial

http://pan.baidu.com/s/1eQf3jvc

把所有有需求的点按DFS排序，需要加的点就是相邻两个点的LCA

妈蛋转眼就高二了

省选一试不好不坏。。不过NOIP挂了。。如果二试不能翻盘的话就要退役了= =

CF打到internationalmaster了 希望能早点打到红名吧

IGM和GM完全不是一个档次的吧= =

半平面交

各种数值算法

数位DP

代码能力

namespace nf//network flow
{
    #define NN 750000
    #define MM 1700000
    inline int min(int a,int b){if(a>b)return b;return a;}
    int ver[NN],next[MM<<1],to[MM<<1],c[MM<<1];
    int source,sink,n,tot=1;
    void addedge(int from,int des,int cap)
    {
		//if(show){printf("from=%d,des=%d,cap=%d\n",from,des,cap);cout<<endl;}
        /*
		if(from==source)printf("addedge <source,%d>,cap=%d\n",des,cap);
        else if(des==sink)printf("addedge <%d,sink>,cap=%d\n",from,cap);
        else printf("addedge <%d,%d>,cap=%d\n",from,des,cap);
		printf("from=%d,des=%d\n",from,des);
		*/
        //++tot;++tot;
        
        next[++tot]=ver[from];to[tot]=des;c[tot]=cap;ver[from]=tot;
        next[++tot]=ver[des];to[tot]=from;c[tot]=0;ver[des]=tot;
        
    }
    int h[NN],vh[NN];long long flow;bool found;
    int isap(int poi,int f)
    {
        if(poi==sink)return f;
        int minh=n-1,uf=f;
        for(int i=ver[poi];i;i=next[i])
        {
            if(c[i]>0)
            {
                if(h[poi]==h[to[i]]+1)
                {
					int tmp=isap(to[i],min(c[i],f));
					f-=tmp;
					c[i]-=tmp;
					c[i^1]+=tmp;
                    if(f==0||h[source]>=n)return uf-f;
                }
                if(h[to[i]]<minh)minh=h[to[i]];
            }
        }
        if(uf==f)
        {
            if(--vh[h[poi]]==0)h[source]=n;
            h[poi]=minh+1;
            vh[h[poi]]++;
        }
        return uf-f;
    }
    long long solve()
    {
        vh[0]=n;
        flow=0;
        while(h[source]<n)
        {
            found=false;
            flow+=isap(source,2100000000);
        }
        return flow;
    }
    #undef NN
    #undef MM
}

给一棵树，每个节点有权值，有若干询问，每次询问某个节点的子树中出现次数大于y的权值x的个数

dfs序上裸莫队可以O(nsqrtn)，平衡树启发式合并O(nlog²n)，线段树合并O(nlogn)，这种类似启发式合并的做法也是O(nlogn)的

sy2006的代码：

#include <cstdio>
#include <algorithm>
#define NE(x, y) ++ne, e[ne]=y, h[ne]=s[x], s[x]=ne
using namespace std;

inline void R(int &x) {
	char ch = getchar(); x = 0;
	for (; ch<'0'; ch = getchar());
	for (; ch>='0'; ch=getchar()) x = x*10 + ch-'0';
}
const int N = 100005;
struct query {
	int k, ans;
} q[N];
int n, m, ne = 0, vt = 0,
	col[N], l[N], st[N], ed[N], sz[N], cnt[N], sum[N],
	s[N], e[N*2], h[N*2], sq[N], hq[N];
void size(int x, int f) {
	sz[x] = 1;
	for (int w=s[x]; w; w=h[w]) if (e[w]!=f)
		size(e[w], x), sz[x] += sz[e[w]];
}
inline void ins(int x) {
	for (int i=st[x]; i<=ed[x]; ++i)
		++sum[++cnt[l[i]]];
}
inline void del(int x) {
	for (int i=st[x]; i<=ed[x]; ++i)
		--sum[cnt[l[i]]--];
}
void solve(int x, int f) {
	st[x] = ++vt; l[vt] = col[x];
	int mx = 0, mf = 0;
	for (int w=s[x]; w; w=h[w]) if (e[w]!=f)
		if (sz[e[w]] > mx)
			mx = sz[e[w]], mf = e[w];
	for (int w=s[x]; w; w=h[w]) if (e[w]!=f && e[w]!=mf)
		solve(e[w], x), del(e[w]);
	if (mx) solve(mf, x);
	for (int w=s[x]; w; w=h[w]) if (e[w]!=f && e[w]!=mf)
		ins(e[w]);
	++sum[++cnt[col[x]]];
	for (int w=sq[x]; w; w=hq[w])
		q[w].ans = sum[q[w].k];
	ed[x] = vt;
}
int main() {
	R(n); R(m);
	for (int i=1; i<=n; ++i) R(col[i]);
	int x, y;
	for (int i=1; i<n; ++i) {
		R(x); R(y);
		NE(x, y); NE(y, x);
	}
	for (int i=1; i<=m; ++i) {
		R(x); R(q[i].k);
		hq[i] = sq[x], sq[x] = i;
	}
	size(1, 0);
	solve(1, 0);
	for (int i=1; i<=m; ++i)
		printf("%d\n", q[i].ans);
	return 0;
}

基本框架十分清晰

考虑每个点被删除的次数，某个点被删一次一定是作为一个轻儿子被删，在与重儿子合并之后所在联通块大小至少*2，故每个点至多被删logn次，所以复杂度保证在O(nlogn)

可以用神奇的复杂度做一些很暴力的事情

感觉跟线段树的合并差不多，不过这个的空间复杂度小多了

这种写法要离线，如果用可持续化线段树维护那个全局数组的话就可以搞成在线。。不过这样跟线段树合并相比并没有什么优势

令G'为残量网络G在缩强连通分量之后的图

一定在最小割方案中的边：<u,v>满流，且在G'中u=S，v=T

可能在最小割方案中的边：<u,v>满流，且在G'中u!=v

对二分图而言

在最大流方案中一定满流的边：<u,v>满流，且在G'中u!=v

在最大流方案中可能满流的边：<u,v>满流，或（<u,v>流量为0，且在G'中u=v）

namespace simplex
{
	int n,m,next[1011];
	//n:varibel m:equation
	double a[11010][1011];
	#define START_POS 1010
	#define INF 210000000000000.0;
	void pivot(int l,int e)
	{
		int t=START_POS;
		double tmp;
		for(int i=0;i<=n;i++)
			if(a[l][i]!=0){next[t]=i;t=i;}
		next[t]=-1;
		tmp=-a[l][e];
		a[l][e]=-1;
		for(int i=next[START_POS];i!=-1;i=next[i])
			a[l][i]/=tmp;
		for(int i=0;i<=m;i++)
		{
			if(a[i][e]==0)continue;
			if(i==l)continue;
			tmp=a[i][e];a[i][e]=0;
			for(int j=next[START_POS];j!=-1;j=next[j])
				a[i][j]+=a[l][j]*tmp;
		}
	}
	double solve()
	{
		while(1)
		{
			long double min=INF;int l=0,e=0;
			for(int i=1;i<=n;i++)
				if(a[0][i]>0){e=i;break;}
			if(e==0)return a[0][0];
			for(int i=1;i<=m;i++)
				if(a[i][e]<0&&a[i][0]<(-a[i][e])*min)
				{min=a[i][0]/(-a[i][e]);l=i;}
			pivot(l,e);
		}
	}
	#undef INF
	#undef START_POS
}

线性基linear base

for(int i=1;i<=n;i++)
for(int j=64;j>=1;j--)
{
	if(a[i]>>(j-1)&1)
	{
		if(!lb[j]){lb[j]=a[i];break;}
		else a[i]^=lb[j];
	}
}

用这个算法可以求出a数组的线性基

线性基 就是原数组所能xor出的一切数这个线性基都能xor出来，不多不少

正确性显然

见莫涛PPT例六解法三

线性基的个数不超过log2V个，且对于每一位i，有且仅有一个线性基在这一位上是1（见构造过程）

注意到这个算法是在线的，可以随时插入一个新数

如果要支持在线的增加一个数/删除一个数/查询当前所有数的线性基 二进制分组(sillycross的数据结构pdf)或者线段树可以做到一次操作O(64*lgn)

------------与XOR本身关系并不大的东西

一个无向图上的一条路径(u---...---v)的xor和，总可以被u到v的任意一条路径xor一些环的xor值得到

------------------------------------

有了这些东西之后基本上就能做题了

http://www.lydsy.com/JudgeOnline/problem.php?id=2322

http://www.lydsy.com/JudgeOnline/problem.php?id=2115

http://poj.openjudge.cn/challenge4/D/

-----------------------------------

是看到最后一道题 才突然发现自己这一块完全不懂的

定根最小树形图朱刘算法直接跑，O(nm)的理论复杂度但事实上应该到不了，加上现在的各种神机，在cf上看CLJ拿朱刘算法跑过n=10w m=10w的图

要求不定根最小树形图的话再建一个虚拟源点，向每个点连一条权值为v的边，要求v大于原图中所有边权之和，然后以虚拟点为根求定根最小树形图，v的取值保证了虚拟点的出边中只有一条会被选中。v的下界是紧的。

相信信仰剪枝的力量

namespace kdtree
{
    int cmp_id,root;
    struct inf
    {
        int lc,rc,p,min[2],max[2],x[2];
        int ind;
        bool able;
    }t[NN];
    bool operator < (const inf& t1,const inf& t2)
    {if(t1.x[cmp_id]==t2.x[cmp_id])return t1.x[1^cmp_id]<t2.x[1^cmp_id];
    return t1.x[cmp_id]<t2.x[cmp_id];}
    int tot;
    void addpoint(int ind,int px,int py,bool able)
    {++tot;t[tot].ind=ind;t[tot].x[0]=px;t[tot].x[1]=py;t[tot].able=able;}
    void updata(int o)
    {
        if(!t[o].able)
        {t[o].min[0]=t[o].min[1]=INF;t[o].max[0]=t[o].max[1]=-INF;}
        else
        {t[o].min[0]=t[o].max[0]=t[o].x[0];t[o].min[1]=t[o].max[1]=t[o].x[1];}
        if(t[o].lc)
        {
            int lc=t[o].lc;
            if(t[lc].min[0]<t[o].min[0])t[o].min[0]=t[lc].min[0];
            if(t[lc].max[0]>t[o].max[0])t[o].max[0]=t[lc].max[0];
            if(t[lc].min[1]<t[o].min[1])t[o].min[1]=t[lc].min[1];
            if(t[lc].max[1]>t[o].max[1])t[o].max[1]=t[lc].max[1];
        }
        if(t[o].rc)
        {
            int rc=t[o].rc;
            if(t[rc].min[0]<t[o].min[0])t[o].min[0]=t[rc].min[0];
            if(t[rc].max[0]>t[o].max[0])t[o].max[0]=t[rc].max[0];
            if(t[rc].min[1]<t[o].min[1])t[o].min[1]=t[rc].min[1];
            if(t[rc].max[1]>t[o].max[1])t[o].max[1]=t[rc].max[1];
        }
    }
    int build(int l,int r,int p,int d)
    {
        int mid=(l+r)>>1;cmp_id=d;
        nth_element(t+l,t+mid,t+r+1);
        t[mid].p=p;
        if(l<mid)t[mid].lc=build(l,mid-1,mid,1^d);
        if(mid<r)t[mid].rc=build(mid+1,r,mid,1^d);
        updata(mid);
        return mid;
    }
    void build()
    {
        root=build(1,tot,0,0);
        for(int i=1;i<=tot;i++)pos[t[i].ind]=i;
    }
    inline int dist_upper(int o,int px,int py)
    {
        if(t[o].max[0]==-INF)return INF;
        int dist=0;
        if(t[o].max[0]<px)dist+=px-t[o].max[0];
        if(t[o].min[0]>px)dist+=t[o].min[0]-px;
        if(t[o].max[1]<py)dist+=py-t[o].max[1];
        if(t[o].min[1]>py)dist+=t[o].min[1]-py;
        return dist;
    }
    inline int dist(int o,int px,int py)
    {if(!t[o].able)return INF;
    return abs(t[o].x[0]-px)+abs(t[o].x[1]-py);}
    int ans;
    inline void query(int o,int px,int py)
    {
        int dl=INF,dr=INF,d0=dist(o,px,py);
        if(d0<ans)ans=d0;
        if(t[o].lc)dl=dist_upper(t[o].lc,px,py);
        if(t[o].rc)dr=dist_upper(t[o].rc,px,py);
        if(dl<dr)
        {
            if(dl<ans)query(t[o].lc,px,py);
            if(dr<ans)query(t[o].rc,px,py);
        }
        else
        {
            if(dr<ans)query(t[o].rc,px,py);
            if(dl<ans)query(t[o].lc,px,py);
        }
    }
    int query(int px,int py)
    {
        ans=INF-1;query(root,px,py);
        return ans;
    }
    void execute(int o)
    {
        o=pos[o];t[o].able=true;
        while(o)
        {
            updata(o);
            o=t[o].p;
        }
    }
    void show(int o)
    {
        if(t[o].lc)show(t[o].lc);
        printf("(%d,%d)\n",t[o].x[0],t[o].x[1]);
        if(t[o].rc)show(t[o].rc);
    }
    void show(){show(root);}
}

upd@2012.1.3：模板居然是错的。摆棋子那道题的数据得是有多弱。

nth_element(t+l+1,t+mid+1,t+r+1);

↓

nth_element(t+l,t+mid,t+r+1);

突然想起来很久以后的一道题，回去翻了翻别人的代码发现kdt有一种奇怪的用法。在2dtree中，记能包住每个点的子树中所有点的最小矩形。要查询在某条直线以下的所有点的权值和的时候，判断这棵子树是不是都在直线以下/以上/穿过。第一第二种情况都可以直接return，第三种情况递归。

完全不懂复杂度。

分类讨论

①f(n)与f(np)之间的关系

②f(np^(k-1))与f(np^k)之间的关系

空间消耗比正常的写法大了好多倍，要记各种奇怪的东西。

在学会正常写法之前先凑合用吧。

例：bzoj2226,bzoj2813（标程没有特判fib[2]=1可以整除所有数）

1、数论

1.25、数位DP

1.5、组合

2、字符串

3、奇怪高维DP

4、计算几何

4.5、单纯形

5、代码能力

	int a[NN],b[NN],n;
	//ax=b(mod c)
	int solve()
	{
		int i,k,d,tmp,tmp2;
		for(i=2;i<=n;i++)
		{
			tmp=a[i-1]-a[i];
			if(tmp<0)tmp=b[i-1]-(-tmp)%b[i-1];
			d=gcd(b[i],b[i-1]);
			if(tmp%d>0)return -1;
			exgcd(b[i]/d,b[i-1]/d,k,tmp2);
			k*=tmp/d;
			if(k<0)k=b[i-1]-(-k)%b[i-1];
			else k%=b[i-1];
			//printf("%d * %d = %d mod %d\n",b[i],k,tmp,b[i-1]);
			//printf("x= %d * %d + %d\n",k,b[i],a[i]);
			a[i]=k*b[i]+a[i];
			b[i]=lcm(b[i],b[i-1]);
			a[i]%=b[i];
			//printf("x mod %d = %d\n",b[i],a[i]);
		}
		return a[n];
	}

                    ①序列莫队

令BLK=sqrt(n);

按照(l/BLK,r)二元组作为关键字排序，然后暴力转移。

                    ②树上莫队

将树转成dfs序列，设dfn[i]为i点在dfs序列上第一次出现的位置，一个树上的询问(u,v)转化成：

void convert(int u,int v)

{

int l=r=0;

if(dfn[u]<dfn[v])l=dfn[u]+1,r=dfn[v];

if(dfn[v]<dfn[u])l=dfn[v]+1,r=dfn[u];

return (Query)(l,r,lca(u,v));

}

一个点出现两次当没出现过算。

令BLK=sqrt(n);

按照(l/BLK,r)二元组作为关键字排序后处理。

                    ③树上带修改的莫队

另加一维时间轴，在x轴、y轴上跑时顺便在时间轴上跑一下就行了。

令BLK=n^(2/3)

按照(l/BLK,r/BLK,time)三元组作为关键字排序后处理。

觉得在getfail()函数里调用gogogo用来生成fail指针可以写的很短。

所有节点的fail指针构成一棵树，一个节点通过fail指针能够到达的所有点，也即这个点所代表的所有点，都在这个点在fail树上到根的路径上。所以dfs之后用数据结构维护一个dfs序列能够快速的支持一些操作。

hzc
(hzc.pas/c/cpp)
 
【题目描述】
  给出N个字符串的集合T（只要两个字符串编号不同就被认为是
不同的字符串），每次操作有三种可能性：
1、  将编号为i 的字符串从集合T中删除。（若T集合中不存
在该字符串则无视该条操作）
2、  将编号为i 的字符串重新加入集合T。（如果该字符串已
经在集合T中则无视该条操作）
3、  给出一个字符串S，求∑ ??(??, ??)
??∈?? 。定义??(??, ??)为字符串
s 在 S 中 出 现 的 次 数 。 （ 比 如
f(“wyxhzcdjmwyxhzcdjm”,”xhzcd”)=2，f(“aaa”,”aa”)=2）
【输入格式】
第一行两个正整数M、N。
接下来N行，每行一个字符串，代表T集合中的字符串。（一开
始所有字符串都在集合中）。
接下来M行，每行一个字符串。如果第一个字符是’-’，代表操作
1；如果第一个字符是’+’，代表操作2；如果第一个字符是’?’代表操
作3。对于操作1和2，在第一个字符之后会紧接着一个整数，代表
操作的字符串编号。对于操作3，在第一个字符之后会紧接着一个字
符串，代表询问的字符串。（第一个字符与接下来的内容之间是没有
空格的）
【输出格式】
  对于每组询问输出一行，代表每个询问的答案。

【数据范围与规定】
对于100%的数据：1≤N,M≤100,000，N个字符串的长度总和以及所
有询问的字符串的长度总和都不会超过1,000,000（?不算在询问的字
符串长度总和之中），给出的N个字符串以及每个询问的字符串都只
由小写字母组成。

这道题差不多就这意思。还有阿狸的打字机。

真棒。

这种考性质的题目在NOI中出过一次之后再出真的会有意义？

sg函数值为0时先手必输，否则先手必胜。

如果游戏图的点数为n，边数为m，则每个点的sg函数值不超过它的度数+1，故所有点的sg函数值和不超过m，所以在算sg的时候暴力就行了反正均摊是O（1）的。

在mod P(p为质数)意义下：

A!

≡ 1 * 2 * ... * (p-1) * p * 1 * ... * (p-1) * p * ... * p * 1 * 2 * ... * (A mod p)

≡((p-1)!)^(A/p)*(A mod P)!*p^(A/p)

喜闻乐见的威尔逊定理

(p-1)!≡{-1,p为质数;

          2，p=4;

          0，otherwise} mod p

或者直接for(i=1;i<=p-1;i++)？

反正都差不多

剩下的部分用O(p)的时间就可以算了

权值在点上。

                             ①

{包含操作：换根，子树查询/修改}

任选根（假定为1）进行dfs，随时记录哪个点是树根。假设要修改/查询的子树为x，当前树根为root，root和x在以根为1的树中有如下四种关系：

一，x为root的子孙，那么（x在（以root为根的树中）的子树）即为（x在（以1为根的树中）的子树），在dfs序上对应一个区间。

二，lca(x,root)!=x&&lca(x,root)!=root，同情况一。

三，x==root，此时要查询的是整棵树，对应区间[1,n]

四，root为x的子孙，令p为x的某个儿子，使得p为root的祖先。那么此时查询的子树即为整棵树去掉（在以1为根的子树中p的子树）的部分。此时的查询对应整个区间[1,n]去掉p的子树对应的区间。

                            ②

{包含操作：换根，子树查询/修改，链查询/修改}

任选根（假定为1）进行重链剖分（对于每条链，并不维护一个数据结构，只是进行形式上的链剖分），并维护其dfs序列，并且每个点在dfs时先递归处理它的重儿子，然后再处理它的轻儿子。

子树查询/修改和①一样处理。

链修改/查询：一条链会被分成O(lgn)条重链上的部分，而每条重链在dfs序列上都是连续的，所以一条链上查询被分成lgn个区间查询。

                           ③

{②+link/cut}

动态树维护链剖分结构，用splay维护dfs序列，虚实边变化时在splay上即时进行修改，使得每个点在dfs序列上的后继都是它的实儿子。

                          番外：

{包含操作：路径修改，子树修改，单点查询，换根}

假设不存在换根操作。

要求存在操作的逆运算。对路径修改(u,v,delta)变成(root,u,delta)+(root,v,delta)+(root,lca(u,v),-delta)。

此时所有链操作的一段都是根节点。

考虑查询时，对查询点u答案可能产生影响的操作只有u的子树中的到根链操作，以及u的祖先的子树操作。

对dfs序列开两棵线段树。子树操作时直接在1线段树中区间修改。到根链操作时在2线段树中单点修改，记下这个操作。

查询时在线段树1中单点查询，在线段树2中区间查询。

要求支持换根操作时同理。

复杂度比上述其他方法都少了个lgn，还好写很多。真是神奇。

滚粗了

D1T1快速幂 T2逆序对 T3最大生成森林上倍增

D2T1贪心 T2线段树优化DP/贪心 T3拆点+堆+dij最短路

第二天T1看错题意。T3没调出来。暴力分给的很足。在大ZJ已滚粗。

希望能卡到线上。

大部分人D2T3都写的无脑n^4bfs。在考场上这种行为显然比较科学，即使还剩下3小时。没写过的东西在考场上写出来的可能性太小。在最后半个小时才开始调我果然太天真。

想想平时模拟赛的时候总是觉得自己能想到题目的解法就行了能不能在时间内写+调出反而不甚在意，总觉得自己在NOIP的时候会很稳健。真是蠢透。

唉。

最后一题的建图真是太恶心。四种情况分类讨论在考场上真让人崩溃。

希望拿到代码能调出来。

也许已经彻底走远了。

满分的欲望强得让我后悔。

讨厌的感觉。

滚回去高考吗。

初中的同学们现在都已经很厉害了。葱物理一等翔已经清华了。只可惜我现在还是个逗比。

不想回班级不想回去看同学们不想在他们的询问下只好表示自己滚粗了。

惨惨惨。

最后留下一点感慨吧。考试的时候绝对不能想着搏一搏发挥出100%的水平，发挥个70%，80%就差不多了。总会有人考挂，而你要做的只是让自己不要成为其中一个。

回想去年NOIP、省选一试，明明什么都不懂却考的相当不错，因为明知道自己不懂，暴力分能拿就拿，正解能打就打打不出来也行。

现在自以为自己已经厉害了对去年的那种屌丝心态不屑一顾却还没有强大到可以像那些教主一样轻松AK。现在这种状态真是太可怕了。

希望能够帮到那些没事情干来看别人博客的后人。

在出发的前一天我把思维导图给了一份学弟，本以为已经消除了死亡flag没想到还是挂了。

发上来吧。http://pan.baidu.com/s/1mWCQH

唉真是黑暗的一天。

两种形式

一、

f(i)=sigma(g(j),j|i)

g(i)=sigma(f(j)*μ(i/j),j|i)

二、

f(i)=sigma(g(j),i|j)

g(i)=sigma(f(j)*miu(j/i),i|j)

在Splay()之前pushdown

在setc()时pushup

也还是挺好写的

    #define NN 100001
    struct inf{int ch[2],r,p;bool rev;}t[NN];
    inline bool isroot(int o)
    {return o==0||(t[t[o].p].ch[0]!=o&&t[t[o].p].ch[1]!=o);}
    inline void pushdown(int o)
    {
        int lc=t[o].ch[0],rc=t[o].ch[1];
        if(t[o].rev)
        {
            int tmp=t[o].ch[0];
            t[o].ch[0]=t[o].ch[1];
            t[o].ch[1]=tmp;
            t[lc].rev^=1;t[lc].r^=1;
            t[rc].rev^=1;t[rc].r^=1;
            t[o].rev=false;
        }
    }
    void pushup(int o)
    {

    }
    inline void setc(int f,int c,int sty)
    {t[f].ch[sty]=c;t[c].p=f;t[c].r=sty;pushup(f);}
    inline void rotate(int o,int sty)
    {
        int x=t[o].ch[sty];
        if(isroot(o))t[x].p=t[o].p;
        else setc(t[o].p,x,t[o].r);
        setc(o,t[x].ch[1^sty],sty);
        setc(x,o,1^sty);
    }
    int stack[NN],top;
    void splay(int o)
    {
        stack[top=1]=o;
        int x=o,y;
        while(!isroot(x)){stack[++top]=t[x].p;x=t[x].p;}
        while(top)pushdown(stack[top--]);
        while(!isroot(o))
        {
            x=t[o].p;y=t[x].p;
            if(isroot(x))
                rotate(x,t[o].r);
            else
            {
                if(t[o].r==t[x].r)
                    rotate(y,t[x].r);
                rotate(x,t[o].r);
            }
        }
    }

void access(int o)
{
	int tmp=0;
	while(o)
	{
		splay(o);
		setc(tmp,o,1);
		tmp=o;
		o=t[o].p;
	}
}

int getroot(int o)
{
	access(o);
	splay(o);
	while(t[o].ch[0])o=t[o].ch[0];
	return o;
}

void setroot(int o)
{
	access(o);
	splay(o);
	t[o].rev^=1;
}

void link(int u,int v)
{
	if(getroot(u)==getroot(v))return;
	setroot(u);
	t[u].p=v;
}

void destory(int u,int v)
{
	access(u);
	splay(v);
	if(t[v].p==u)t[v].p=0;
	else
	{
		access(v);
		splay(u);
		if(t[u].p==v)t[u].p=0;
	}
}

尿都给虐出来了

惨遭题解党殴打

学军怎么这么厉害

P1：军训

 

HYSBZ 开学了！今年 HYSBZ 有 n 个男生来上学，学号为 1… n，每个学生都必须

参加军训。在这种比较堕落的学校里，每个男生都会有 Gi 个女朋友，而且每个

人都会有一个欠扁值 Hi 。学校为了保证军训时教官不会因为学生们都是人生赢家

或者是太欠扁而发生打架事故，所以要把学生们分班，并做出了如下要求：

1.分班必须按照学号顺序来，即不能在一个班上出现学号不连续的情况。 

2.每个学生必须要被分到某个班上。 

3.每个班的欠扁值定义为该班中欠扁值最高的那名同学的欠扁值。所有班的欠

扁值之和不得超过 Limit。 

4.每个班的女友指数定义为该班中所有同学的女友数量之和。在满足条件 1、

2、3 的情况下，分班应使得女友指数最高的那个班的女友指数最小。 

请你帮 HYSBZ 的教务处完成分班工作，并输出女友指数最高的班级的女友指数。 

输入数据保证题目有解。

1<=n，G i <=20000，1<=Hi，Limit<=10^7

此百团大战非彼百团大战也。这指的是HYSBZ的社团开始招人了。若若的LMZ现在站在操场上，有很多很多个社团在操场上排成一排。有些社团为了吸引人们加入，会表演节目。而现在LMZ拿到了节目单，有n个节目，其描述了在T_i时刻X_i号社团会表演节目（持续时间忽略不计）。而LMZ在一单位时间内最多也只能跑过V个社团的距离（比如从1号社团跑到V+1号社团），而最少则可以不动，跑步的左右方向任意。他想知道：

1.    当他初始时刻是站在0号社团的情况下，他最多能看到多少节目？

2.    当他初始时刻可以站在任意位置的情况下，他最多能看到多少节目？

注：初始时刻指的是时间为0.

1<=n<=100000，-2*10⁸<=X_i<=2*10⁸，1<=V<=1000，1<=T_i<=10⁶

 

P4：选课

  你真的认为选课是那么容易的事吗？HYSBZ的ZY同志告诉你，原来选课也会让人产生一种想要回到火星的感觉。假设你的一周有n天，那么ZY编写的选课系统就会给你n堂课。但是该系统不允许在星期i和星期i+1的时候选第i堂课，也不允许你在星期n和星期一的时候选第n堂课。然后连你自己也搞不清哪种选课方案合法，哪种选课不合法了。你只想知道，你到底有多少种合法的选课方案。

n<=100000

分治的一个重要技巧是每次递归的复杂度必须只能和当前处理的子树大小有关，所以flag的清零啊什么的都要把扫过的点重新扫一遍。

如果把已经处理过的子树和当前子树看作两棵子树的话点分治还是挺好写的。

把已经扫过的子树中的所有点记录到一个序列中，如果需要重新扫这棵子树那么就扫那个序列，可以让程序快不少。

还是很担心如果考试考到点分治会被卡成暴力分。

终于调出来了。

细节太多。。就算想清楚原理和实现细节实现出来还会有一千万个错。。

#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <queue>
using namespace std;
int map[12][12],n,m;//m列n行 

char tmp[10];bool endofline;
std::queue<int> q[2];bool flag[2][900];
int findr[10][900],findl[10][900];

int get(int num,int i){return num&(1<<i);}
bool isleft(int num,int i){return get(num,2*i-2)>0;}
bool isright(int num,int i){return get(num,2*i-1)>0;}
bool isempty(int num,int i){return (!isleft(num,i))&&(!isright(num,i));}

int index(int x,int y){return (x-1)*m+y;}
int change(int num,int i,int v1,int v2)
{
	if((v1==1)^(get(num,2*i-2)>0))num^=(1<<(2*i-2));
	if((v2==1)^(get(num,2*i-1)>0))num^=(1<<(2*i-1));
	return num;
}
int stk[11],pos[11],top;
int zip[300000],unzip[900],tmpl[11],tmpr[11];
int f[2][900],ind;
bool check(int state)
{
	int i;
	for(i=1;i<m;i++)if(!isempty(state,i))return false;
	if(isleft(state,m)&&isright(state,m+1))return true;
	return false;
}
void updata(int from,int t)
{
	if(endofline)
	{
		if(!isempty(unzip[t],m+1))return;
		int newstate=unzip[t]<<2;
		t=zip[newstate];
	}
	f[1^ind][t]+=f[ind][from];if(!flag[1^ind][t]){q[1^ind].push(t);flag[1^ind][t]=true;}
}
void clear()
{
	memset(f,0,sizeof(f));
	memset(flag,0,sizeof(flag));
	while(!q[0].empty())q[0].pop();
	while(!q[1].empty())q[1].pop();
}
void solve()
{
	int i,j,cnt=0,state,newstate,ans=0;bool legal;
	for(j=0;j<(1<<(2*(m+1)));j++)
	{
		top=0;legal=true;
		for(i=1;i<=m+1;i++)
		{
			if(isleft(j,i)&&isright(j,i)){legal=false;break;}
			if(isleft(j,i))
			{
				stk[++top]=1;
				pos[top]=i;
			}
			else if(isright(j,i))
			{
				if(top==0||stk[top]==2){legal=false;break;}
				if(stk[top]==1)
				{
					tmpr[pos[top]]=i;
					tmpl[pos[top]]=0;
					tmpl[i]=pos[top];
					tmpr[i]=0;
					top--;
				}
			}
			else tmpl[i]=tmpr[i]=0;
			
		}
		if(top>0)legal=false;
		if(legal)
		{
			++cnt;unzip[cnt]=j;zip[j]=cnt;
			for(i=1;i<=m+1;i++){findl[i][cnt]=tmpl[i];findr[i][cnt]=tmpr[i];}
		}
		else zip[j]=0;
	}
	for(i=0;i<n;i++)
	{
		scanf("%s",tmp);
		for(j=0;j<m;j++)
			map[i+1][j+1]=(tmp[j]=='.');
	}
	n++;map[n][1]=1;map[n][m]=1;
	for(i=2;i<m;i++)map[n][i]=0;
	n++;for(i=1;i<=m;i++)map[n][i]=1;
	q[1].push(1);f[1][1]=1;
	for(i=1;i<=n;i++)for(j=1;j<=m;j++)
	{
		ind=index(i,j)&1;
		memset(flag[ind^1],0,sizeof(flag[ind^1]));
		memset(f[ind^1],0,sizeof(f[ind^1]));
		endofline=(j==m);
		while(!q[ind].empty())
		{
			state=q[ind].front();q[ind].pop();
			state=unzip[state];
			if(map[i][j]!=1)
			{
				if(isempty(state,j)&&isempty(state,j+1))
					updata(zip[state],zip[state]);
				continue;
			}
			if(i==n&&j==m)
			{
				if(check(state))ans+=f[ind][zip[state]];
				continue;
			}
			if(isempty(state,j)&&isempty(state,j+1))
			{
				newstate=change(state,j,1,0);
				newstate=change(newstate,j+1,0,1);
				updata(zip[state],zip[newstate]);
			}
			//-#
			if(isright(state,j)&&isempty(state,j+1))
			{
				updata(zip[state],zip[state]);
				newstate=change(state,j,0,0);
				newstate=change(newstate,j+1,0,1);
				updata(zip[state],zip[newstate]);
			}
			if(isleft(state,j)&&isempty(state,j+1))
			{
				updata(zip[state],zip[state]);
				newstate=change(state,j,0,0);
				newstate=change(newstate,j+1,1,0);
				updata(zip[state],zip[newstate]);
			}
			//#-
			if(isempty(state,j)&&isleft(state,j+1))
			{
				updata(zip[state],zip[state]);
				newstate=change(state,j,1,0);
				newstate=change(newstate,j+1,0,0);
				updata(zip[state],zip[newstate]);
			}
			if(isempty(state,j)&&isright(state,j+1))
			{
				updata(zip[state],zip[state]);
				newstate=change(state,j,0,1);
				newstate=change(newstate,j+1,0,0);
				updata(zip[state],zip[newstate]);
			}
			//--
			if(isright(state,j)&&isleft(state,j+1))
			{
				newstate=change(state,j,0,0);
				newstate=change(newstate,j+1,0,0);
				updata(zip[state],zip[newstate]);
			}
			if(isleft(state,j)&&isleft(state,j+1))
			{
				newstate=change(state,j,0,0);
				newstate=change(newstate,j+1,0,0);
				newstate=change(newstate,findr[j+1][zip[state]],1,0);
				updata(zip[state],zip[newstate]);
			}
			if(isright(state,j)&&isright(state,j+1))
			{
				newstate=change(state,j,0,0);
				newstate=change(newstate,j+1,0,0);
				newstate=change(newstate,findl[j][zip[state]],0,1);
				updata(zip[state],zip[newstate]);
			}
			/*
			if(isleft(state,j)&&isright(state,j+1))
				if(i==n&&j==m)ans+=f[ind][zip[state]];
			*/
		}
	}
	printf("%d\n",ans);
}
int main()
{
	while(scanf("%d %d",&n,&m)!=EOF)
	{
		if(n==0&&m==0)break;
		clear();
		solve();
	}
}

#include <cstdio>
#include <cstdlib>
#include <cstring>
#define NN 100001
int rank[NN],n,sum[NN];
int sa[NN],str[NN];
int trank[NN]={0},tsa[NN]={0};
void sort(int k)
{
	memset(sum,0,sizeof(sum));
	int i;
	for(i=1;i<=n;i++)sum[rank[i+k]]++;
	for(i=1;i<=n;i++)sum[i]+=sum[i-1];
	for(i=1;i<=n;i++)trank[i]=sum[rank[i+k]]--;
	for(i=1;i<=n;i++)tsa[trank[i]]=i;
	
	memset(sum,0,sizeof(sum));
	for(i=1;i<=n;i++)sum[rank[i]]++;
	for(i=1;i<=n;i++)sum[i]+=sum[i-1];
	for(i=n;i>=1;i--)trank[tsa[i]]=sum[rank[tsa[i]]]--;
	for(i=1;i<=n;i++)sa[trank[i]]=i;
	
	trank[sa[1]]=1;
	for(i=2;i<=n;i++)
		if(rank[sa[i]]!=rank[sa[i-1]]||rank[sa[i]+k]!=rank[sa[i-1]+k])
			trank[sa[i]]=trank[sa[i-1]]+1;
		else trank[sa[i]]=trank[sa[i-1]];
	for(i=1;i<=n;i++)rank[i]=trank[i];
}
int main()
{
	scanf("%d",&n);
	int i,k;for(i=1;i<=n;i++)scanf("%d",&str[i]);
	for(i=1;i<=n;i++)sum[str[i]]++;
	for(i=1;i<=n;i++)sum[i]+=sum[i-1];
	for(i=1;i<=n;i++)rank[i]=sum[str[i]-1]+1;
	for(k=1;2*k<=n;k<<=1)sort(k);
	for(i=1;i<=n;i++)sa[rank[i]]=i;
}

终于写成了。

和普通splay的不同主要在select这个函数还有在访问一个节点之后都要pushdown,修改/旋转后都要updata。

void select(int k,int aim)
{
	int o=root;pushdown(o);
	while(t[t[o].ch[0]].siz+1!=k)
	{
		if(t[t[o].ch[0]].siz+1>k)
			o=t[o].ch[0];
		else{k-=t[t[o].ch[0]].siz+1;o=t[o].ch[1];}
		pushdown(o);
	}
	if(aim!=root)
	{
		int tmp=root;
		root=aim;t[aim].f=-1;
		splay(o);
		root=tmp;setc(o,root,1);
	}
	else splay(o);
}

建树的时候建成一棵平衡的比较好。

请让我做一个悲伤的表情。

第一题题目意思理解错了- -。序列是连续的还是不连续的啊。。。

第二题敲了70分朴素。。。后来发现其实满分做法也不难想。

第三题贴吧里说极小值有坑。。。考试的时候看到极小值，一想f(0)=f(n)=0，就很高兴得认为等价于f(i)>=0.后来yzd来讲才突然发现说的是极小值均为0.

于是就这么考挂了。

考挂自己弱。。。

唉。

接下来要好好努力了。。。不能让明年有遗憾。

基本上一整天都待在数实。真的挺无聊的。。如果没有人陪着就更无聊了吧。已经开始玩MC了不知道接下来会怎么样。数实这种东西就偶尔来一次兴奋不已，整天待着就无聊的要死了。

跟假期在家里百无聊赖一个意思。

CP真是为了奖金不择手段。

WTF。

早上还是学了点东西的。

扩展GCD、中国剩余定理、高斯消元以及解xor方程组、大步小步算法、线性筛、pollard-rho。

扩展gcd没什么好说的。理解起来一点难度都没有，能自己推出来的。

-----------------------------------------------------------------

高斯消元就跟平时解方程一个意思。把平时的过程一般化就是高斯消元了。

xor方程大同小异，把+/-运算变成xor就行了。

如果出现[0 0 0 0 0 0|0]那么就说明有冗余方程。如果出现[0 0 0 0 0 0 0|x](x!=0)那么说明无解。

如果消元到最后产生的上三角矩阵的行数比列数小，即有效方程数小于未知数的数量，那么就产生自由元。自由元只是一个相对的概念。一个方程组的自由元数量是一定的，但是自由元的选取方案不唯一。

对于xor方程组来说一个自由元意味着方程组解的数量*2.

-----------------------------------------------------------------

中国剩余定理的模板题小学的时候经常被作为奥术题，我还都做不出来。事情是这样的。方程组由{x=bi(mod ci)}组成。令M=c1*c2...*cn。对于第i条方程来说我们试图寻找这么一个di使得：di=k*(M/ci)，且di=1(mod ci)。设di=1+y*ci，那么方程变成：k*(M/ci)=y*ci+1。想办法解这玩意就可以得到一个k，那么di=k*(M/ci)。那么x=sigma(di*bi) Mod M就是方程的一个解。这也蛮明显的。构造性的算法真心巧妙。

-----------------------------------------------------------------

大步小步算法是个很暴力的东西。用来求x使得a^x=b(mod p)的。

如果p是质数，或者说p与a互质，那么：

任意取一自然数m(m<=p)。可令x=k*m-r，其中(m>r>=0)。代入方程：a^(k*m)=b*(a^r)(mod p)。

将r从0循环到m-1，计算出所有b*(a^r)(mod p)，然后把每一个取值所对应的r存在一个哈希表里。如果p比较大就开map，如果p比较小就直接用数组把。并且这个取值和r不是一一对应的，但是这并无大碍。然后计算a^m，并且将k从1循环到(p/m)，对于每一个k计算出a^(k*m)，然后在哈希表中寻找有没有对应的r存在。如果存在那么就找到了一个解x=k*m-r。

如果用map做哈希表：效率O((m+n/m)logm)。在m=[sqrt(n)]时效率最高。

这种分块求解【或者说大步小步】的思想很有用。

-----------------------------------------------------------------

线性筛：

先上代码

#define NN 100000
#define PRIME_IN_N 5000
bool flag[NN];
int prime[PRIME_IN_N],tot;
void Eular_Griddle()//Linear Griddle
{
	int i,j;
	for(i=2;i<=n;i++)
	{
		if(!flag[i])prime[++tot]=i;
		for(j=1;j<=tot;j++)
		{
			if(i*prime[j]>n)break;
			flag[i*prime[j]]=true;
			if(i%prime[j]==0)break;
		}
	}
}

与平时我们写的筛法对比：

#define NN 100000
#define PRIME_IN_N 5000
bool flag[NN];
int prime[PRIME_IN_N],tot;
void Normal_Griddle()//O(NloglogN)
{
	int i,j;
	for(i=2;i<=n;i++)
	{
                if(flag[i])continue;
                prime[++tot]=i;
		for(j=i;j<=n/i;j++)
			flag[i*j]=true;
	}
}

基本上是一个意思。主要的区别在这里：if(i%prime[j]==0)break;

欧拉线性筛的效率保证在于每个数都只被筛中一次，而且是被它的最小质因数筛掉的（即n=i*prime[j]中的prime[j]是它的最小质因数）。曷故哉？

注意到prime[]是递增的，而且我们在第一次满足(i%prime[j]==0)时就break了，即此时的prime[j]是i的最小质因数（如果i是质数，那么就会把整个循环做完）。之前提到prime[j]必须为prime[j]*i的最小质因数才能保证效率。那么为了保证prime[j]*i的最小质因数是prime[j]，我们必须让prime[j]比i的最小质因数要小。这就是这一句话的含义。

这种线性筛比原来的筛法好了一些，效率提高，而且还能顺便求出每个数的最小质因数。这样就可以对一些积性函数求值了。

-----------------------------------------------------------------

pollard-rho。是一个寻找n的因子的方法。基于这个事实：如果a不为n的倍数，那么gcd(a,n)为n的一个因子。

I、选取一个x1

II、利用函数计算出x2使得x2-x1不被n整除。

III、如果gcd(x2-x1,n)>1那么找到因子，结束过程

IV、否则重复I。

----------------------------------------------------------------

觉得我的表达能力真是逆天了这些东西被我讲得好简单。看线性筛的时候蛋疼死我了。当然也可能是因为现在理解了所以看自己的解释觉得顺理成章- -。

惨惨惨。

总结写完了这下彻底没事情干了。

期中考惨跪。接下来要考省选Day2了呢。最近好迷茫啊。右手不知道怎么搞的一打代码或者拿鼠标就有强烈的抽筋呕吐恶心感。小学弟们要来了呢。一年过得好快。眨眼就要高二了。想什么时候把OI的知识体系做成一张图以后学起来会有方向性一点。

希望省选D2不要跪。

差分约束系统是拿来获得一些形式特殊的不等式的特解的。这种不等式的形式是xi<=xj+c。注意必须有等号。如果题目中是严格小于那么+/-eps即可。如果是其他形式…想办法变形成这样吧。如果没法变形成这样…那应该不是差分约束的题目- -。

做法是把每一个变量xi看作一个点Ai，记从某个点O出发到Ai的最短路长度为di。那么很显然，如果存在边<u,v>=w那么du+w>=dv，即dv<=du+w。那么就把不等式组中的每一条不等式{xi<=xj+c}变成一条边<Aj,Ai>，权值为c。

注意到这些建图与出发点O的选取无关，而任意选取一个点O所计算出的d数组都满足原不等式组，即为一组解。

那么就可以在这张图上求一些特殊的解了。【这张图很有可能不是连通的。】

如果建出的图中有负圈，那么就没有d数组，也即原不等式没有解。判负圈可以用spfa或者karp等等算法。

那么如果没有负圈，原不等式组就存在解。

对于起点O点的选取决定了求出的是怎样的一组特解。

如果要求解中两个变量的差值xi-xj最大，那么选取Aj作为起点计算最短路。【如果Ai与Aj不连通那么它们的取值就不相关，差值就可以任意小。】

---------------------------------------------------------------------------------

一些小技巧。

如果要求两个变量的差值xi-xj最大，那么反过来就是要求差值xj-xi最小。

如果题目中的一些不等式是规则的【例如xi-x(x+1)>=1】，那么不要把这些不等式所转换成的边加入边集中，而是在处理每个点的时候特殊处理这些规则的边。这么做可以减少内存消耗，而且不知道为什么速度大大提高。

从长沙回来就到绍兴去zjoi了。

飞机到杭州再坐的大巴去绍兴。杭州机场的快餐很好吃。

听了两天课整天被题目虐。对clj用的那个思维导图软件很感兴趣【好像很炫酷的样子】。见到了seter真人。长得好萌。还见到了何奇正真人版。好小好萌的样子。

涨了姿势。替罪羊树…大杀器hash…如何卡大杀器hash…后缀数组在字符串题目中的重要性…

考试的时候rp大爆发。第一题第一次写树套树。之前从来没有理解过的东西在考场上突然理解了。对拍能过的时候很高兴。

第二题看样子是写挂了。。。

第三题只做了di=1的情况。。。是个dp。

然后总分就180了。与noip成绩加权平均之后排在16th。在省队15人名单之外。

只能期盼day2翻盘了。

要是day1考爆了。。哪有现在这么多麻烦。

中间有好多天都没写了。

后期考的比较烂。而且也越来越懒就不想写了。

总分rank6.前面的那几个人都好厉害。我和第五名差了100分，第四名和第三名差了300分。可见一斑。

现在在机场，飞机延误了。没事干就总结一下。【哦刚才因为没有身份证的原因折腾了好久。跟负重3000米跑差不多。damnit回去我就要办身份证。】

这次认识了好多好厉害的人。见到了好多好神的题目。骗分水平提高了不少。居然还用一个多项式算法在一个NPC问题里莫名其妙得了60分。我应该得60%的图灵奖- -

最高考到过rank2.已经挺满足了。没有爆过0.也挺高兴的。

最近整天写代码手指都有抽筋的倾向。

得了一件衣服挺高兴的。但是是短袖所以最近应该穿不了。

回忆一下，主要还记得的学到的东西：分块【莫队】，线段树的合并【这玩意好像在主席WC讲了之后到处用这货出题？节操丧尽】，乘法逆元【之前自以为明白，没想到互质与不互质的情况要分开。吓傻了。】，原根【在数实的题目里见过原根的应用，应该算是基础知识吧】，网络流的一些建模【这玩意完全是在YY】，树的分治【强烈感觉这会是个大坑】，kd-tree【- -被杨国烨大神虐出翔】，随机算法【感谢随机帝在最开始两天的AC教会了我们这种神奇的骗分。虽然用这玩意没有骗到过任何一分。】，还有各种题目的乱搞。

之前每天上课的时候都有记笔记，但是出发的时候弄丢了。

马上就省选了。好紧张。希望能正常发挥吧。

End.

边的流量有上下界的最大流/费用流：

I、二分

I.从汇点T到源点S连边，下界为f上界oo。二分此下界f。

II.建立新网络（无下界有源有汇，新建源点s',汇点t'），每一条新边(u,v)的容量即为原图中(u,v)边的上界减下界。

III.对于每一个点u，令M=（入u边的下界和）减去（出u边的下界和），如果M非负则连边(s',u)，容量M，如果M为负则连边(u,t')，容量-M。称这种新加的边为附加边。

IV.对新网络以s'为源t'为汇求最大流，如果每一条附加边都满载，那么原网络存在一个流量至少为f的可行流。

II、直接做

I、从汇点T到源点S连边，下界0上界oo。

II.建立新网络（无下界有源有汇，新建源点s',汇点t'），每一条新边(u,v)的容量即为原图中(u,v)边的上界减下界。

III.对于每一个点u，令M=（入u边的下界和）减去（出u边的下界和），如果M非负则连边(s',u)，容量M，如果M为负则连边(u,t')，容量-M。称这种新加的边为附加边。

IV.在新网络里以s’为源t’为汇求最大流，如果每一条附加边都满载那么原网络存在可行流。然后再在残量网络中以s为源t为汇求最大流。那么求得即为原网络最大流。如果要求最小流，那么以t为源s为汇求最大流。费用流是一个意思的。

__今天的题目基本不可做。

所以就没什么好讲的了- -。

题目见cena包。比较难的第一第二题都是shoi的原题。第三题比较简单就不给题解了。

------------------------------------------------------------------

最近写总结越来越偷懒了。

-----------------------------------------------------------------

也可能是因为最近心情不太好。

-----------------------------------------------------------------

今天悲剧了。

-----------------------------------------------------------------

end.

- -不想写Day5了。Day6放假一天。所以就Day7了。

长沙的雨好大。

今天运气不错rank2了。到今天为止总分好像是rank4还是rank5…和前一名差了100分左右吧。逐渐和大神们混熟了。

今天太晚了就偷懒一下吧。题目和题解见cena包。

说一些除了题解之外的东西。

第一题罗神说可以用线段树的合并做。如果每棵线段树都只建有用的节点，没用的节点用0号节点代替，那么合并的总复杂度可以保证在O(nlogn)。戳这里了解更多

第二题确实坑爹。那两个结论很不靠谱的样子即使猜到了考试的时候一般不敢用。还好当时只想着骗分。。。没想到就a了。注意一些常数上的优化，比如如果一大一小两个质数在合并之后比合并之前还要糟糕那么费用流中这条边就没必要建。然后一开始的时候用贪心获取一个解，再用网络流修正结果。这么做之后可以比标程快20倍。

第三题题解居然这么暴力。杨国晔大神说可以用kd-tree做。什么时候去了解看看。

眨眼间就Day4了。很快就可以回去了~

---------------------------------------------------------------------------

还是吃不惯辣。可是居然还没上火。

--------------------------------------------------------------------------

今天考得不错到了rank5。

-------------------------------------------------------------------------

第一题：

给出一棵树，每个节点有权值，有若干个查询，每次查询要求输出树上从u到v的路径上如果把权值a看成权值b那么有几种不同的权值出现。(n<=50000,m<=100000,1<=权值<=n，有20%的数据n<=100,40%的数据是一条链。)

【这一看就是COT2的加强版。没做过cot2只知道cot2很神。想了想应该是莫队算法的树上版，但是没写过。于是对小数据暴力，对链的数据用树状数组和函数式线段树做到了离线O(mlogm+nlogn)。或者就是像标程那样去把树转成DFS序列然后用莫队算法。

讲一下在链上的O(mlogm+nlogn)的离线算法。先假设不存在那个奇怪的（将某一权值看成另一权值）。把所有询问都读入存起来，然后根据右端点排序。对于每一个元素Ai，设pre=最大的j使得Aj=Ai。那么这个数能够对左端点在[pre+1,i]范围内的查询贡献1个不同的权值。所以就用一个树状数组维护一下前缀和就好了。然后再把那个奇怪的限制加进来。这个限制只能够在（查询区间中权值a和权值b都出现了）的时候影响答案，并且会让答案-1.那么还剩下一个问题，即给出一个区间[l,r]，判断某一个权值有没有出现于其中。那么建一棵函数式线段树就能在O(logn)解决一次查询。所以总复杂度就是O(nlogn+mlogm)】

第二题：

- -尼玛题面太复杂了而且太难。这种奇怪的自动机模型- -。自己去看评测包吧。

第三题：

定义一个数优美：这个数的各个数位可以被分成两组，使得这两组之和相等。求区间[l,r]中有多少个数优美。(l,r<=10^9)

【- -这种题出得好失败简直为打表而生。可惜当时不敢打10000个数的表不然就AC了- -。正解是这样的：因为一个数优美与否只与组成它的各位数有关，所以这个数将其重排列之后是否优美与原数相同。于是就可以生成所有各位数递增的优美数，发现在10^9范围内只有1W个左右，那么对于每一个数枚举其排列看看有多少在查询范围内即可。】

--------------------------------------------------------------------------------

今天又是我发cena包。好高兴。没有在昨天发了cena包之后遭到悲惨下场。

早上起来晚了。早饭很悲戚一点都不好而且连早饭里都是辣椒。这里的人真重口味。然后中饭晚饭因为师大附中的人来上课所以所有菜都有海量辣椒，连汤都没了。这么辣真捉急。

-----------------------------------------------------------------------------------------------

今天考的不错rank2了。哈哈终于我能发cena包了。到这里几天，感觉自己写朴素写搜索写随机的能力强了不少- -

----------------------------------------------------------------------------------------------

第一题：

从前有一位旅者，他想要游遍天下所有的景点。这一天他来到了一个神奇的王国：在这片土地上，
有n个城市，从1到n进行编号。王国中有m条道路，第i 条道路连接着两个城市ai,bi，由于年
代久远，所有的道路都已经不能使用。如果要修复第i条道路，需要wi的时间。为了更好的旅
行，旅者想要将某些道路修复，使得1号城市能够到达n号城市，2号城市能够到达n-1号城市..k
号城市能够到达n-k+1号城市。为了满足他的要求，请问最少需要多少时间去修复道路。无解请输
出-1。 (n,m<=10000,k<=4)

【k小得很蹊跷。标程的解法是把这2*k个点的连通性情况用状态压缩记录，然后转化成最短路（或者说dp？差不多一个意思）。考试的时候我没想到是状态压缩。第一眼看过去就敲了个最小生成树然后在最小生成树上贪心。但是在2个小时后被自己造了一组数据卡掉了。最后一个小时写了个费用流的变种。这题给我这么一种感觉：如果不考虑1一定要到n，2一定要到n-1，…，而是只要求从1,2,…,k，走到n,n-1,…,n-k+1，那么直接计算这么一个网络上的最小费用最大流即可：一个超级源与1,2,…,k分别连边容量1费用0，其他所有边的容量无限大费用为其长度，然后一个超级汇与n,n-1,…,n-k+1分别连边容量1费用0.并且这个网络里的边只有在流量由0变为1或1变为0时才产生相应费用，其他情况不产生费用。因为这个网络很特殊每次增广流量最大+1，所以改写spfa即可。不过不知道为什么wa60分。 [updata@13.3.22：这个算法完全是错的。因为不能保证如果一开始不存在负圈那么不管怎么增广永远不会出现负圈。所以连费用流的基本要求都无法满足。当时居然给我拿了60分。。。数据太弱- -]】

第二题：

山的模型如下：山由一个顶点集：A1,A2…An给定，保证Ai的x单调递增。我们将Ai 和Ai+1 之间连上线段，表示山的某一段。Pty想要爬到这座山的最高的顶点，当两个顶点的高度相同时，我们认为x比较大的顶点要高一些。Pty不是盲人，所以他将会在爬山时采取一些策略，使得他能够尽量快的到达最高的顶点。Pty从初始的顶点出发，往左右看去，他将朝他能够看到的最高的顶点方向走去。当走到每一个顶点时，他都会重新观察，如果这时看到的顶点比之前看到的顶点还要高，那么他将选择此时看到的顶点走去，直到他到达最高点为止。如果顶点A能够看到顶点B，则不存在某条线段和线段AB严格相交。Pty想知道从每一个顶点出发，分别需要经过几个顶点才能到达最高点。(n<=300000，输入保证xi递增，hi<=10^6)

【这题给我的第一感觉跟noip2012Day1T3很像。嗯…都是有高度的一些点…都是有人在走来走去…数据还都这么大一看就不能暴力。根据那一题的经验，应该先预处理出每一个点向左或者向右会到哪个点，然后再倍增就可以知道每个点的答案。根据数据大小分析…效率应该是O(nlogn)的。首先要解决预处理。获取一个点左边的最高的能看到的点，还有一个隐藏条件，即那个能看到的最高点还要满足比当前站的位置要高。这个原因很简单就不说了。那么就可以从左到右扫描用斜率单调的栈维护一个上凸包来预处理一个点向左会看向哪里。右边同理。效率O(n)的。

嗯到此为止效率很让人满意。但是这里讨厌的是这个走路的人很容易走到一半看到更高的就马上改变主意了，所以这个人第一次停下来并不一定是走到了他看到的那个位置，也有可能是在第一个使他改变主意的位置。所以根据每个点向左看到哪里要计算出他最终会向左走到哪里第一次停下来。这个地方可以用rmq+二分位置O(nlog^2n)来做，也可以在对所有点按照能看到的高度从低到高排序后双向链表来做O(nlogn+n)。{双向链表在那一题里也可以用。}那么就获得了每一个点第一次会停在哪个点，并且这中间经过了几个点也能知道。那么接下来{I、可以照着那一题的做法，倍增来做。O(nlogn)}{II、可以发现每个点只能走向一个点，并且每个点最终都会走向山顶。所以这些连线构成了一棵树，并且边权都已知，那么直接bfsdfs都可以做了。O(n)}。所有有两种方法地方我都写的是蠢一点的那个- -。但是不知道怎么搞的写挫了WA70分。】

第三题：

在神秘的东方有一棵奇葩的树，它有一个固定的根节点（编号为1）。树的每条边上都是一个字符，字符为a,b,c中的一个，你可以从树上的任意一个点出发，然后沿着远离根的边往下行走，在任意一个节点停止，将你经过的边的字符依次写下来，就能得到一个字符串，例如： 在这棵树中我们能够得到的字符串是： c, cb, ca, a, b, a
现在pty得到了一棵树和一个字符串S。如果S的一个子串[l,r]和树上某条路径所得到的字符串完全相同，则我们称这个子串和该路径匹配。现在pty想知道，S的所有子串和树上的所有路径的匹配总数是多少？ (n<=800000,S<=800000)

【这题是后缀自动机。下午讲的后缀自动机至今不懂。悲惨下场。】

-------------------------------------------------------------------------------------------------

之前两天发cena包的人第二天都遭到了悲惨下场。希望明天不要挂。

早上起来心情很好。【悲剧的前奏。。。

--------------------------------------------------------------------

考试的时候只写了第二第三题，第二题写了个满分算法，第三题写了一个随机化算法。结果第二题的BFS写跪了。然后就跪了。然后运气不佳随机一分都没有。然后就没有然后了。

----------------------------------------------------------------------

第一题：

给出一个无根树。树有N个点，边有权值。每个点都有颜色，是黑色、白色、
灰色这三种颜色之一，称为一棵三色树。
可爱的Alice觉得，一个三色树为均衡的，当且仅当，树中不含有黑色结点
或者含有至多一个白色节点。然而，给出的三色树可能并不满足这个性质。
所以，Alice打算删去若干条边使得形成的森林中每棵树都是均衡的，花费
的代价等于删去的边的权值之和。请你计算需要花费的代价最小是多少。

(n<=300000，5组数据以内，时限2s)

【树形动归。状态还要加上子树中白色与黑色节点的颜色。 考试的时候怎么没想到呢- -

第二题：

给出一张无向图，每条边连接两个不同的点，且长度是已知的。而逃犯Frank选择了一条
从城市1到城市N的最短路径作为他的逃跑路线。
为了阻止Frank，共和国总统决定在某些点的边的出入口设立检查
点，在Frank经过检查点时将他逮捕。
举例来说，如果有一条边连接点u和点v，在这条公路的城市u
或城市v的出入口设立检查点，那么Frank经过此边时就会被发现。
特别的是，由于点N实际上处在反对派的控制下，所以不能在点N设立
检查点。

然而在任何城市设立检查点都需要一定的费用。更具体的，若在城市u设立
k个检查点，就要花费Au乘以k的代价，其中Au是城市u的相关参数。值得注意
的是，这个代价与这k个检查点具体设在哪些公路的出入口无关。于是，总统责令情报局拟定一个方案，花费最小的代价使得无论Frank选择
哪条最短路线，都会在（除城市N以外）某个城市的高速公路出入口被发现。

注意，我们称两个方案不同当且仅当存在某城市k，两种方案中在城市k的
检查点的设置（而不仅是数目）是不同的。

求解两个问题：一、最小花费。二、最优方案是否唯一。(V<=400,E<=4000)

【网络流。第一问和最小割模型很像，但是不完全相同。对图跑一次spfa，求出每个点到1的最短路径，只保留那些du+c(u,v)=dv的边，然后将其流量定为min(Au,Av)，且An=INF，那么此网络的最小割即最大流即为最小花费。可惜只做第一问一分都没有。第二问事实上是在问此网络的最小割方案是否唯一。有好多种方法可以做这件事。

{I、枚举每一条在当前最小割内的边，将其容量+1，广搜一次看看有没有增广路。如果存在增广路那么说明原边一定在此图的任意一个最小割方案里。原因如下，这条边的容量改变对那些不包含这条边的最小割方案没有影响，也即原图的最小割在容量改变前后不变。如果存在这种方案，那么一定找不到增广路。因为最小割=最大流。所以只要当前最小割里的每一条边都在任意最小割里，最小割就是唯一的。效率O(E^2)。}

{II、以下操作均作用于求了最大流之后的残量网络。从源点BFS标记每一个到达的点。从汇点逆向BFS标记每一个到达的点。如果存在既在当前最大流上，又没有被标记到的点，那么此网络的最小割是不唯一的。充分性和必要性都证明一次即可。注意最小割的方案一定是（最大流中满载的边）的一个子集。效率O(E)}】

第三题：

Alice是个很有魅力的人，她一共有N个好朋友。而她的这些好朋友互相之
间可能认识，也可能不认识，还可能有矛盾。
这N个人之间是否认识是无所谓的，但是如果两个人之间存在矛盾就会产生
一些问题。这里，矛盾关系是双向的。
Alice知道，如果她邀请的任意一个好朋友小X在宴会上仅看到一个与小X
有矛盾的人小Y，就会不太高兴，不过可以假装没看见。但是，如果小X再次
看到另一个与小X有矛盾的人小Z，小X就会很生气并离开宴会。
为了防止这样的情形出现，Alice决定只邀请她的一部分好朋友参加宴会，
使得对于这些人中的任意一个人，至多有一个与他（或她）有矛盾的人同时受到
邀请。这样，就不会有人中途离开宴会了。问最多可以同时邀请几个人。(n<=40,50组数据以内)

【先证它是NP问题，即它的一个解可以在多项式时间内判断其是否合法。这是显然的。然后再证它可以规约到一个NPC问题即任意图的最大独立集。所以这是一个NPC问题。标程搜索。然后又证明了存在一个最优方案使得所有（只与一个人有矛盾的人）都被邀请。在此结论的基础上剪枝搜索。然后昨天随机AC第三题的随机帝今天又AC了此题。用的还是随机。神一样的男人。】

----------------------------------------------------------------------------

悲惨下场。

在计算一个很大的组合数modP时会用到乘法逆元。即把/a变成*(f(a))，其中f(a)为a在模P意义下的乘法逆元，即a*f(a) mod P=1

计算乘法逆元有两种方法，扩展gcd或基于欧拉公式的快速幂取模。

------------------------------------------------------------------------------------------------------

扩展gcd就是求解方程ax=1(mod P)的最小整数解.

设ax=1+y*p，即a*f(a,p)=1+p*g(a,p)，把x和y的解看成关于a,p的函数。

a>=p时，设a=p*k+r，则式子变成：

p*k*f(a,p)+r*f(a,p)=1+p*g(a,p)，移项，得r*f(a,p)=1+p*(g(a,p)-k*f(a,p))

那么就得到f(a mod p,p)=f(a,p)，g(a mod p,p)=g(a,p)-[a/p]*f(a,p);

p>=a时差不多一个意思。

所以把f,g设成全局变量，像普通gcd那样做，即时更新f,g即可。

----------------------------------------------------------------------------------------------------

设欧拉函数phi(x)=在[1,x-1]中与x互质的数字个数。那么欧拉公式：

a^phi(P)=1(mod P)

两边同除a,即可得到a^(phi(P)-1) mod P即为a在模P意义下的乘法逆元。

特例：

如果P是质数，那么phi(P)=P-1.即a的乘法逆元为a^(P-2)，快速幂即可。

昨天晚上做了一个奇怪的梦，梦见今天考试怒得5分稳稳垫底。然后考试一开始看到第一题有20个测试点，当时就吓尿了。

第一题：

给出一个无限大的矩阵，每个格子的值c如下给出：

I、1     (x==0||y==0)

II、c[x-1][y]+c[x][y-1]   (else)

求从[0][0]到[n][m]的一条路径，使得这条路径上的点权和最小，输出点权和mod 10^9+7

(m,n<=10^12,m*n<=10^14,时限1s)

-------------------------------------------------------------------------------------------------------------

第二题：

给定一个非负整数序列{a}，初始长度为N。
有M个操作，有以下两种操作类型：
1、A x：添加操作，表示在序列末尾添加一个数x，序列的长度N+1。
2、Q l r x：询问操作，你需要找到一个位置p，满足l<=p<=r，使得：
a[p] xor a[p+1] xor ... xor a[N] xor x 最大，输出最大是多少。(m,n<=300000,时限2s)

----------------------------------------------------------------------------------------------------------------------------

第三题：

一家公司需要雇佣一些工人来进行生产。
在他们手里有N个可以雇佣的工人资料，这些工人有些曾经合作过，他们
在一起工作能够使公司利润更大，而有些工人素未谋面，不能给公司带来什么额
外的收益。我们用P(i,j)来衡量i 工人和j 工人一起雇佣能给公司带来的收益，P
越大公司收益越高。
当然，公司雇佣工人需要支付薪金；然而，在这里公司需要支付的薪金并不
与雇佣的人数成正比，而是满足：C=K*(200-K)。其中C表示需要支付的薪金，
K表示雇佣的人数。
现在，为了让公司能够有最多的获利，需要最大化G=S/C，其中S表示雇佣
的工人两两P(i,j)之和，C表示公司需要支付的薪金。

(n<=50,时限1s)

-------------------------------------------------------------------------------------------------------------

第二第三题交的都是朴素。第一题想+写了两个小时，用到乘法逆元，加了很多惨无人道的优化之后ac时间排到第一。好高兴。

然后总分就rank9了- -

-------------------------------------------------------------------------------------------------------------

官方题解：

一、

观察原图，将x+y值相同的点(x,y)归为一层，将层按x+y值从小到大看，会发现其实整个图是杨辉三角的一部分。

容易看出，每层权值最小的点或都在最左侧或都在最右侧。由于N,M互换并不影响答案，所以假如每层权值最小的点都在最右侧，则交换N,M，保证每层权值最小的点都在最左侧。

从本质上说，就是该图的最短路是确定的，都是沿着矩形外围一圈走，且一开始先走矩形长的一边。(下述C均为组合数)

保证N<=M，那么答案可以直接算出，也就是M+C[M][0]+C[M+1][1]+…+C[M+N][N]。

C[M][0]=1；

C[M+1][1]=(M+1)/1；

C[M+2][2]=(M+1)*(M+2)/(1*2)=C[M+1][1]*((M+2)/2)；

C[M+3][3]=C[M+2][2]*((M+3)/3)；

…

C[M+N][N]=C[M+N-1][N-1]*((M+N)/N)。

由于模的数是一个素数，所以除以数a直接转化成乘数a的逆元。接着直接递推即可。

【注：这里的算法不是最优的。容易知道sigma(C(i,a),i=[1,b])=C(b,a+1)。那么效率顿时就提高了很多。】

==============================================================

二、

可以用线段树套字母树做到O(Nlog^2N)，下面讲O(NlogN)的做法。

首先对原序列求前缀异或和，记为S[i]。则对于询问l,r,x，则是在S[l-1]..S[r-1]这些数中找到一个数，和X异或的结果最大。

要使异或结果最大，可以从高位到低位看X的二进制位，如果该位为1，则我们需要找这些数中是否存在该位为0的。

假如我们将S[l-1]..S[r-1]这些数按照二进制从高到低的顺序看做字符串，并做出这些字符串对应的字母树，那么我们可以在O(log)时间内解决问题。

问题在于如何快速查找S[l-1]..S[r-1]形成的字母树的信息，并且支持在序列末尾添加的操作。

由于我们在字母树查询的只是“该结点是否存在至少一个在[l-1,r-1]范围的数”，而[l-1,r-1]的个数是满足区间减法的。也就是说，如果我们知道[0..r-1]以及[0..l-2]在该节点的个数，那么我们可以通过区间减法得到[l-1,r-1]的信息。

即我们需要对每个位置X，维护[0,X]的字母树，而注意到[0,X]到[0,X+1]，在字母树上只添加了一个字符串，修改的结点个数不会超过O(log)；而我们利用函数式编程的思想，每次修改并不在原结点修改，而是新建一个修改过的结点。这样我们可以保留这个字母树的历史版本，可以在O(NlogN)的时间内解决这道题。

时间复杂度：O(NlogN)。空间复杂度：O(NlogN)。

【注：第一次见到用trie来做数字统计类题目的。函数式的思想很棒。此题有人朴素得了50分。膜拜常数帝。】

=============================================================

三、

题目需要使得 sigma(P)/(K*(200-K)) 最大。

首先，我们可以二分答案X，那么我们需要判断的是，是否存在点集，使得sigma(P)/(K*(200-K)) > X。

我们对式子做以下变形：

我自然的想到将边权重新赋值为P(i,j)+2*X，将点权赋值为-199X，那么问题转换成在新图上选出一个点集，使得导出子图的点权与边权的和最大。

解决的方法之一是将其转换成最大权闭合子图的模型：

我们构造一个新图以转换模型，原图中的一个点u对应新图中的一个点u，点权不变；对于原图中的边e(u,v)，对应新图中点e，点权为原图的边权，并且新图中e点向u点和v点连接有向边，表示若选择e，则u和v也一定被选。

然后我们在求出新图的最大权闭合子图就可以判断是否能够满足sigma(P)/(K*(200-K)) > X这个式子了。

【注：这题的01分数规划模型很明显，但是可惜考场上没有成功转化为最小割。毕竟题目做得太少。这题有人贪心AC，有人写了个随机模拟爬山法也AC了。当时考场上怎么没想到随机呢- -】

-------------------------------------------------------------------------------------------------------------

食堂的菜逐渐变得不那么辣。挺好吃的。这里的人说话口音好重。

-------------------------------------------------------------------------------------------------------------

听说总分前20会有T恤。希望能有。期待明天的考试。

struct node{int ch[2],fa,val,right;}t[MN];
int tot=0,root;
int build(int v){t[++tot].val=v;t[tot].right=0;return tot;}

void setc(int f,int c,bool r){t[f].ch[r]=c;t[c].fa=f;t[c].right=r;}
void rotate(int o,int sty)//sty=0 left
{
	int x=t[o].ch[sty],f=t[o].fa;
	if(o==root){root=x;t[x].fa=0;t[x].right=0;}
	else setc(f,x,t[o].right);
	setc(o,t[x].ch[sty^1],sty);
	setc(x,o,1^sty);
}

void splay(int o)
{
	int f,g;
	while(o!=root)
	{
		f=t[o].fa;g=t[f].fa;
		if(f==root){rotate(f,t[o].right);return;}
		if(g&&t[f].right==t[o].right)
			rotate(g,t[f].right);
		rotate(f,t[o].right);
	}
}

所谓01分数规划是这么一个问题：

定义f=sigma(ai*xi)/sigma(bi*xi)，xi可以取{0,1}，可能还有一些限制条件比如x1=1时x2!=1，而目标是让f最大/最小化（保证bi,ai>0）。下面以最大值为例。

直接做并没有什么太好的办法，在此考虑将原式变形，sigma(ai*xi)=f*sigma(bi*xi)，继续变形得到sigma[xi*(ai-f*bi)]=0

令g(f)=sigma[xi*(ai-f*bi)]

考虑到bi>0，因此对于一组确定的决策xi来说，g(f)为一个斜率<0的一次函数，因此如果g(fnow)>0，那么就表明这组决策xi比当前fnow的决策更优。

由此衍生出两种算法：二分与dinkelbach算法

二分：每次二分一个fnow，想办法选取一组xi使得g>0（并且满足限制条件），如果成功那么移动下界，否则移动上界。

dinkelbach：先随便定一组决策，然后想办法选取一组xi使得g>0（并且满足限制条件），那么用新的决策替换老的决策。

dinkelbach的时间复杂度是不稳定的，天知道要几步才能爬到最优决策，而二分是稳定的。

----------------------------------------------------------------------------------------------------------

分数规划的题目框架都是一致的，不同的地方在于选取xi并且要求其满足限制条件的那一步。这一步的处理应该才是命题人比较看重的。

以【最优比率生成树】为例。每条边选取有代价和权值，要求权值和除以代价和最大。

每次二分出来一个fnow，计算各条边的wi=-（ai-f*bi），用prim计算最小生成树，如果最小生成树的sigma(wi)>0那么移动下界，否则移动上界。

----------------------------------------------------------------------------------------------------------

01分数规划问题到了这里变得很像01背包，那么相应得还能有各种背包问题在分数规划上的对应【完全分数规划、部分分数规划等等】，但是均可在01分数规划的基础上贪心解决，不再叙述。

----------------------------------------------------------------------------------------------------------

在开始之前，先阐述距离标号的定义。后文中距离标号有两个定义，故此明确：

①在最大流部分，u点距离标号du定义从源点（或汇点）开始BFS第一次搜到u点的时间（即为经过的最少边数）

②在费用流部分，u点距离标号du定义为源点（或汇点）到u点的最短路径（将边的费用视为距离）

形式化的定义，对于任何点u，v∈V有du<=dv+w(v,u)（性质1），并且至少有一个点v可以使等号成立（性质2）。将使du=dv+w(v,u)的边(v,u)称为可行边。在最大流部分，w(v,u)即为1（如果边(v,u)存在）；在费用流部分w(v,u)即为边(v,u)的费用c（如果边(v,u)）存在。

                                                I、最大流

                                                     -----------只是一个引子

还记得EK、dinic、ISAP么？。

求网络中最大流的算法有两个体系：增广路系和预流推进系。增广路系的核心就是不断地寻找增广路直到网络中不再存在增广路，而增广路系算法的变化只是在于如何找增广路。

EK：每次用广搜寻找一条最短的增广路（即包含最少的边），然后沿其增广。

                                         ↓

dinic：同样是寻找一条最短的增广路，但是并不需要每次都广搜。EK算法每次广搜所获得的信息并没有被完全利用，因此dinic将其改进，用广搜获得每个点到源点的距离标号，增广时沿距离标号严格减1的路径增广，直到网络中不再存在这么一条路径，那么重新广搜计算距离标号，如果广搜发现整个源点到汇点已经不连通那么退出算法。

                                         ↓

ISAP：与dinic一样基于距离标号，不过这里保存的是到汇点的距离标号。并且考虑每次增广对网络的影响，发现增广只会使点的距离标号变大，并且并不会破坏距离标号的性质1，只会破坏性质2。找不到可行边就是因为性质2被破坏。那么重新修补性质2的方法也很简单，并不需要重新计算整个图的距离标号，只需要调整距离标号：如果从u点开始寻找增广路没有成功，即u点的距离标号的性质2被破坏，那么在所有<u,v>（v∈V）中找到距离标号最小的一个v，使du=dv+1即可。

                                             II、最小费用最大流

                                                      -----------真正的东西

算法I：最小费用最大流一般使用的是基于SPFA的增广路算法，即每次用spfa计算图的距离标号，然后沿着可行边进行增广。

                                         ↓

算法II（原始对偶算法）：根据最大流和费用流算法的对应，这里应该存在一个类dinic算法，即并不每次都用spfa重新计算整个图的距离标号，而是在图中不再存在由可行边组成的增广路时再进行一次SPFA重新计算点的距离标号，如果源点与汇点不再连通那么退出算法。这个算法因为dinic算法的存在而变得显然。然后有一个优化，即只有在第一次计算距离标号时用spfa，之后对距离标号的修正可以在对边重赋权之后dijkstra做。

                                         ↓

算法III（zkw费用流）：zkw费用流算法可以视为ISAP算法在费用流问题上的映射算法。这里距离标号同样记录的是到汇点的。每次增广，同样不会破坏距离标号的性质1，只会破坏性质2。并且被破坏的点并没有很多（只有在增广路上的点有可能被破坏）。因此并不需要SPFA来重新计算全部的距离标号。如果某一次寻找可行边组成增广路的尝试进行到点u失败，那么在所有的边<u,v>（v∈V）中找到距离标号最小的一个v，使du=dv+c<u,v>即可。

                                            III、最小费用最大流的算法分析

算法I和EK算法是如此的类似，不妨称其为E'K'算法。算法II因为介于算法I与算法III中间，不予评价。称算法III为zkw算法。

zkw本人是这么说的：

这里（E'K'算法-----zkw算法的比较）与（EK算法-------ISAP算法的比较）完全相同，产生差异的原因也相同。举个例子，如果一个网络最大的可能流量只有2，那么判断此网络的最大流到底是多少，EK算法就会快于ISAP算法。

考虑到ISAP完全碾压EK算法，zkw算法也是可以碾压E'K'算法的。

                                            IV、最小费用流算法的优化

                                                         ---------------照葫芦画瓢，形似也就能神似

这里我们试图加快zkw算法的速度。

在求解最大流问题中，常见的对ISAP算法的优化有：当前弧优化、多路增广、gap优化与程序开始执行时的一次BFS来直接给各点确定一个距离标号。

那么如果迁移到最小费用最大流问题中，当前弧优化显然还是能用的，因为一条边有可能沿其增广多次；多路增广也能用；而程序开始执行时先计算一次各点的距离标号也是合理的，但是gap优化在最小费用最大流中就不能用了。

最近两天写了几道树链剖分，终于能够写出一个两百行的程序不用陷入无尽调试了。

树链剖分需要对于每个点求出如下几个域：

dep：此点深度

siz:此点子树的点数

fa：此点的父亲

son：此点重儿子的编号

top：此点所在重链顶端的点编号

w：如果题目要维护的权值在点上：表示此点在所在重链中的编号

   如果题目要维护的权值在边上：表示此点与其父亲的连边在其所在重链中的编号

belong：此点（或此点与其父亲的连边）所属重链的编号

weight：此点（或此点与其父亲的连边）的权值

-----------------------------------------------------------------------------

这些东西的求出可以用两次DFS求，也可以用一次BFS生成BFS序列，再对序列正反两次扫描得到。但是由于树链剖分的题点数较大，DFS可能爆栈，故推荐BFS方法。

-----------------------------------------------------------------------------

对于每一条重链可以用线段树维护，但需要考虑空间消耗问题。也可以把所有的链放在一个线段树里维护，但是会加大常数。

-----------------------------------------------------------------------------

对于一个查询(u,v)来说，可以先求LCA再逐步提升两个点，也可以这么做：

令f1=top[u],f2=top[v]，如果f1==f2那么两个点已经在一条链上，链内查询；否则不妨设dep[f1]<=dep[f2]，则先链内查询将v提至f2,然后通过一条轻边将f2提至fa[f2]，重复此过程。

这么做最后两个点一定都停在他们的LCA处，因此树链剖分也可以用来在线求LCA，每一条重链不加任何数据结构维护，空间消耗O(n)。

----------------------------------------------------------------------------

永远不要用std::vector来存储边。

----------------------------------------------------------------------------

树链剖分一般长度会有150+。但是写熟之后就没什么感觉了。

----------------------------------------------------------------------------

END。

树上的问题：

----1、块状树

----2、DFS序

----3、树链剖分

----4、倍增

----5、主席树

----QTRE、COT系列

----6、树的分治---》点分治，边分治

网络流建图

1、最大流

2、最小割

3、最大权闭合子图

4、等式或不等式（部分线形规划）

5、凸费用流

6、上下界流

Burnside&Polya

1、矩阵乘法加速线形递推式

可持续化数据结构

1、可持续化线段树

刚刚在做poj2528。想起来以前傲妹让我们写的那一道usaco题，两道题都是在平面【直线】上用矩形【线段】覆盖，最后计算有几个矩形【线段】没有被完全覆盖。

usaco那道题n只有1000，但是大家都被这种题目吓傻了纷纷去写线段树，写出来的效率还都是O(n^2logn)的。当时我写的O(nlogn)的扫描线线段树，没考虑一种特殊情况导致整个算法是错的，但是数据弱居然也有80分。现在想来这题的最优算法应该是nlogn的扫描线线段树，每个节点储存该线段当前的矩形及被当前矩形覆盖的最上矩形。

这算法效率是最优的但是写起来很麻烦。当时被傲妹给出的标程之短震惊了。

矩形切割的想法很简单，即矩形与矩形相交的并也可以分割为若干个矩形。用递归来写很方便。矩形切割的想法在一维上的实现，即线段切割，在线段树七题里莫诺瑞根那道题的效率比线段树还高。

矩形\线段切割的最坏效率O(n^2)，但是能导致这种最坏效率的数据需要手工构造，确实比较麻烦。出题人一般也不会蛋疼到去刻意卡这种算法吧。【跟spfa还能用的理由差不多

想起来很简单，但是判断相交那里有很多种情况要考虑，貌似比较麻烦。后来发现，排除掉相离的情况，剩下的情况比较少，用4条语句每次考虑一条边的相交情况即可。

poj2528用线段切割写起来只有25行，235MS1A。效率不怎么样但是确实短。

#include <cstdio>
int l[10001],r[10001],n,ans=0;
bool sf(int A,int B,int dep)
{
    if(dep==n+1)return true;
    if(B<l[dep]||A>r[dep]) return sf(A,B,dep+1);
    bool f=false;
    if(A<l[dep]){f=f|sf(A,l[dep]-1,dep+1);A=l[dep];}
    if(r[dep]<B) f=f|sf(r[dep]+1,B,dep+1);
    return f;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        ans=0;
        scanf("%d",&n);
        for(int i=1;i<=n;i++) scanf("%d %d",&l[i],&r[i]);
        for(int i=n;i>=1;i--) if(sf(l[i],r[i],i+1)) ++ans;
        printf("%d\n",ans);
    }
}

试着写一点东西看看。。。好像挺不错的- -

从此以后不再使用堆式写法。空间时间双重还写起来那么麻烦。

新写法和平衡树的写法比较接近。

namespace SGT
{
    int lc[NN],rc[NN],val[NN],p[NN],tot=0,lnk[MM];
    void build(int l,int r,int pa)
    {
        int now=++tot;p[now]=pa;
        if(l==r){lnk[l]=now;return;}
        lc[now]=tot+1;build(l,MID(l,r),now);
        rc[now]=tot+1;build(MID(l,r)+1,r,now);
    }
}